En este blog te hablaremos de la factorización, su definición, los diferentes casos y presentamos ejemplos prácticos.

¿Qué es?

La factorización consiste en descomponer un número entero o una expresión algebraica como el producto de 2 o más factores.

Para el caso de número enteros, se factorizan como el producto de 2 o más número primos. Los números primos son aquellos que únicamente se dividen entre 1 y él mismo.

Los números primos = {2, 3, 5, 7, 11, 13…}

Ejemplo:

 

 

 

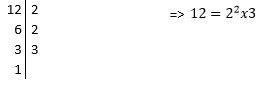
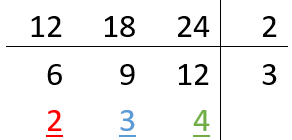
Factorizar un número es expresarlo como producto de dos o más números primos.

Por ejemplo:

Queremos factorizar el número 12. Comenzamos a dividirlo entre el número primo más pequeño que es el 2:

12÷2 = 6

Nos da como resultado 6, pero ese número no es primo, por lo que lo dividimos entre un número primo también: 6÷2 = 3.

Debido a que el número 3 también es primo, el resultado de factorizar el número 12 es:

12 = 2 x 2 x 3; también se puede escribir

Factorización por factor común.

El factor común se refiere al monomio que es el máximo común divisor de todos los términos de un polinomio. Por ejemplo:

Factorizar 

Primero se calcula el mínimo común divisor (M.C.D) de los coeficientes. En este caso es 6.

 

 

 

Como x se repite en cada término se escoge con su menor exponente: 2. El factor común es:

La expresión algebraica se factoriza como:

 

Diferencia de cuadrados

La factorización de una diferencia de cuadrados está formada por un binomio, un término positivo y uno negativo. Ambos términos deben de tener una raíz cuadrada exacta. Por ejemplo:

Primero se saca la raíz cuadra de cada término:

Posteriormente, ambos términos se ponen dentro de los paréntesis, y en un paréntesis se pone el sino positivo y en el otro el negativo de la siguiente forma:

Factorización por trinomio cuadrado perfecto (TCP)

Se conoce como trinomio cuadrado perfecto a las expresiones algebraicas de 3 términos, cuyo primer y tercer término tienen son cuadrados perfectos, es decir, tienen una raíz cuadrada exacta, y el segundo término es el doble del producto de las raíces cuadradas. Por ejemplo:

Factorizar

Para factorizar un TCP primero debemos extraer las raíces cuadradas del primer y último término.

Raíz cuadrada de      Raíz cuadrada de

Para comprobar si la ecuación es un trinomio cuadrado perfecto se realiza el doble del producto de las raíces cuadradas obtenidas.

Si el resultado es igual al segundo término del trinomio, entonces es un TCP, y el resultado de la factorización es el cuadrado de la suma de la raíz cuadrada del primero y raíz cuadrada del tercer término, quedando así:

Si quieres aprender más o resolver dudas de matemáticas, con gusto puedes visitarnos. Tenemos para ti clases de regularización en matemáticas, física y química para que resuelvas todas tus dudas en los temas que más se te compliquen.

Nosotros estamos convencidos que una atención presencial  con el acompañamiento académico correcto es la solución. Contáctanos.